В пеших путешествиях и велопоездках незаменимым спутником исследователя является топографическая карта. Одной из задач картографии (одной из дисциплин такой науки как геодезия) является изображение криволинейной поверхности Земли (фигуры Земли) на плоской карте. Для решения этой задачи необходимо выбрать эллипсоид — форму трехмерного тела, приближенно соответствующего земной поверхности, датум — начальную точку системы координат (центр эллипсоида) и начальный меридиан (англ. prime meridian) и проекцию — способ изображения поверхности этого тела на плоскости.

Эллипсоиды и датумы

В разное время для построения карт использовались различные варианты представления поверхности Земли в виде сферы или эллипсоида.

Представление Земли в виде сферы радиусом 6378137 метра (либо 6367600 метров) позволяет определить координаты любой точки на земной поверхности в виде двух чисел — широты $\phi$ и долготы $\lambda$:

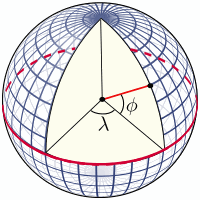
Для земного эллипсоида в качестве (географической) широты используется понятие геодезическая широта (англ. geodetic latitude) φ — угол, образованный нормалью к поверхности земного эллипсоида в данной точке и плоскостью его экватора, причем нормаль не проходит через центр эллипсоида за исключением экватора и полюсов:

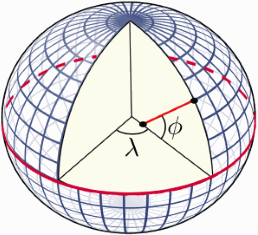
Значение долготы (англ. longitude) λ зависит от выбора начального (нулевого) меридиана для эллипсоида.
В качестве параметров эллипсоида обычно используются радиус большой (экваториальной) полуоси a и сжатие f.
Сжатие $f = {{a-b} \over a}$ определяет сплюснутость эллипсоида у полюсов.

Одним из первых эллипсоидов был эллипсоид Бесселя (Bessel ellipsoid, Bessel 1841), определенный из измерений в 1841 году Фридрихом Бесселем (Friedrich Wilhelm Bessel), с длиной большой полуоси a = 6377397,155 м и сжатием f = 1:299,152815. В настоящее время он используется в Германии, Австрии, Чехии и некоторых азиатских и европейских странах.

Фридрих Бессель

датум Potsdam (PD)

• эллипсоид — Бесселя (Bessel 1841)
• нулевой меридиан — Гринвичский меридиан (Greenwich prime meridian), полное название — United Kingdom Ordnance Survey Zero Meridian
  
  отметка Гринвичского меридиана

Ранее для построения карт в проекции UTM использовался международный эллипсоид (International ellipsoid 1924, Hayford ellipsoid) с длиной большой (экваториальной) полуоси a = 6378388 м и сжатием f = 1:297,00, предложенный американским геодезистом Джоном Филлмором Хейфордом (John Fillmore Hayford) в 1910 году.

Джон Филлмор Хейфорд

датум ED 50 (European Datum 1950)

• эллипсоид — International ellipsoid 1924
• нулевой меридиан — гринвичский меридиан (Greenwich prime meridian)

Для выполнения работ на всей территории СССР с 1946 года (постановление Совета Министров СССР от 7 апреля 1946 г. № 760) использовалась геодезическая система координат СК-42 (Пулково 1942), основанная на эллипсоиде Красовского с длиной большой (экваториальной) полуоси a = 6378245 м и сжатием f = 1:298,3. Этот референц-эллипсоид назван в честь советского астронома-геодезиста Феодосия Николаевича Красовского. Центр этого эллипсоида сдвинут по отношению у центру масс Земли примерно на 100 метров для максимального соответствия поверхности Земли на европейской территории СССР.

Феодосий Николаевич Красовский

датум Пулково-1942 (Pulkovo 1942)

• эллипсоид — Красовского (Krassowsky 1940)
• нулевой меридиан — гринвичский меридиан (Greenwich prime meridian)

В настоящее время (в том числе и в системе GPS) широко используется эллипсоид WGS84 (World Geodetic System 1984) с длиной большой полуоси a = 6378137 м, сжатием f = 1:298,257223563 и эксцентрисетом e = 0,081819191. Центр этого эллипсоида совпадает с центром масс Земли.

датум WGS84 (EPSG:4326)

• эллипсоид — WGS84
• нулевой меридиан — опорный меридиан (IERS Reference Meridian (International Reference Meridian)), проходящий в 5,31″ к востоку от Гринвичского меридиана. Именно от этого меридиана отсчитывается долгота в системе GPS (англ. GPS longitude)
  

Центр системы координат WGS84 совпадает с центром масс Земли, ось Z системы координат направлена на опорный полюс (англ. IERS Reference Pole (IRP)) и совпадает с осью вращения эллипсоида, ось X проходит по линии пересечения нулевого меридиана и плоскости, проходящей через точку начала координат и перпендикулярную к оси Z, ось Y перпедикулярна оси X.

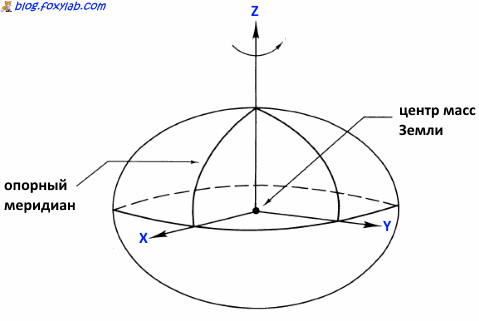
система координат WGS84

Альтернативой эллипсоиду WGS84 является эллипсоид ПЗ-90, используемый в системе ГЛОНАСС, с длиной большой полуоси a = 6378136 м и сжатием f = 1:298,25784.

Преобразования датумов

При простейшем варианте перехода между датумами Пулково-1942 и WGS84 необходимо учитывать только смещение центра эллипсоида Красовского по отношению к центру эллипсоида WGS84:
рекомендовано в ГОСТ 51794-2001 —
dX = +00023,92 м; dY = –00141,27 м; dZ = –00080,91 м;
рекомендовано в World Geodetic System 1984. NIMA, 2000 —
dX = +00028 м; dY = –00130 м; dZ = –00095 м.
Следует отметить, что выше приведены усредненные значения коэффициентов, которые для более точного преобразования должны вычисляться для каждой точки земной поверхности индивидуально. Например, для соседней с Беларусью Польшей эти параметры таковы:
dX = +00023 м; dY = –00124 м; dZ = –00082 м (по данным User’s Handbook on Datum Transformations involving WGS-84, 3-е издание, 2003)
Такое преобразование называется трехпараметрическим.
При более точной трансформации (преобразовании Молоденского) необходимо учитывать разницу между формами эллипсоидов, определяемую двумя параметрами:
da — разница между длинами больших  полуосей, df — разница между коэффициентами сжатия (разница в уплощении). Их значения одинаковы для ГОСТ и NIMA:
da = – 00108 м; df = + 0,00480795 ⋅ 10^-4 м.

Михаил Сергеевич Молоденский

При переходе между датумами ED 50 и WGS84 параметры преобразования таковы:
da = – 00251 м; df = — 0,14192702 ⋅ 10^-4 м;
для Европы dX = -87 м; dY = –96 м; dZ = –120 м ( по данным User’s Handbook on Datum Transformations involving WGS-84, 3-е издание, 2003).

Набор из указанных пяти параметров (dX, dY, dZ, da, df) может вводиться в навигатор или навигационную программу в качестве характеристики используемого пользователем датума.

Проекции

Способ изображения трехмерной земной поверхности на двумерной карте определяется выбранной картографической проекцией.
Наиболее популярны (нормальная) цилиндрическая проекция Меркатора и такая ее разновидность как поперечно-цилиндрическая проекция Меркатора (Transverse Mercator).

Герард Меркатор

В отличие от известной в течение веков нормальной проекции Меркатора, которая особенно хороша для изображения экваториальных областей, поперечная проекция отличается тем, что цилиндр, на который проецируется поверхность планеты, повернут на 90°:

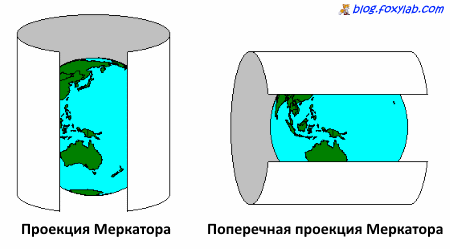
Цилиндрическая проекция Меркатора

Сферическая проекция Меркатора

Для сферической проекции действуют следующие формулы перевода широты $\phi$ и долготы $\lambda$ точки на поверхности земной сферы (в радианах) в прямоугольные координаты $x$ и $y$ на карте (в метрах):
$x = (\lambda — {\lambda}_0) \cdot R$ ;
$y = arcsinh ( \tan ( \phi ) ) \cdot R =\ln { (  \tan{ ( {\phi \over 2} + {\pi \over 4} } ) } )  \cdot R$
(logarithmic tangent formula) ,
где $R$ — радиус сферы, ${\lambda}_0$ — долгота нулевого меридиана.
Масштабный коэффициент $k$ представляет собой отношения расстояния по сетке карты (англ. grid distance) к локальному (геодезическому) расстоянию (англ. geodetic distance):
$k = {1 \over {\cos \phi}}$.
Обратный перевод реализуется с помощью таких формул:
$\lambda = {x \over R} + {\lambda}_0 $ ;
$ \phi = {\pi \over 2} — 2 \arctan(e^{-y \over R}) $ .
Важной для мореплавания особенностью проекции Меркатора является то, что линия румба (англ. rhumb lines) или локсодрома (англ. loxodrome)  на ней изображается прямой линией.
Локсодрома — это дуга, пересекающая меридианы под одним и тем же углом, т.е. путь с постоянным (локсодромическим) путевым углом.
Путевой угол, ПУ (англ. heading) — это угол между северным направлением меридиана в месте измерения и направлением линии пути, отсчитывается по часовой стрелке от направления на географический север (0° применяется для указания направления движения на север, 90° — на восток).
Локсодромы являются спиралями, совершающими неограниченное число витков, приближаясь к полюсам.

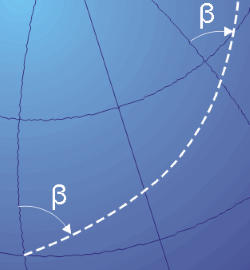
локсодрома

Следует отметить, что локсодрома не является кратчайшим путем между двумя точками — ортодромой, дугой большого круга, соединяющей эти точки.

Web Mercator

Вариант меркаторовской сферической проекции используется многими картографическими сервисами, например, OpenStreetMap, Google Maps, Bing Maps.

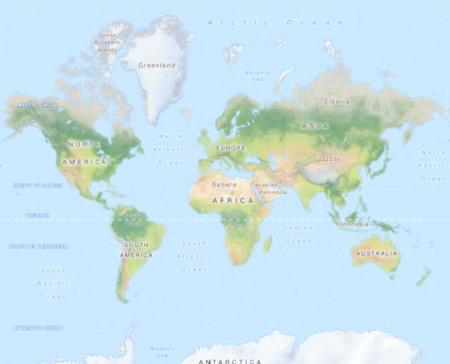
карта мира в OpenStreetMap

В OpenStreetMap карта мира представляет собой квадрат с координатами точек по осям x и y, лежащими между  -20 037 508,34 и 20 037 508,34 м. Как следствие, на такой карте не показаны области, лежащие севернее 85,051129° северной широты и южнее 85,051129° южной широты. Это значение широты $\phi_{max}$ является решением уравнения:
$\phi_{max} =  2\arctan(e^\pi ) — {\pi\over 2} $ .
Как и любой карте, составленной в проекции Меркатора, ей свойственны искажения площадей, наиболее ярко проявляющиеся при сравнении изображенных на карте Гренландии и Австралии:

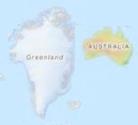
При прорисовке карты в OpenStreetMap координаты (широта и долгота) на эллипсоиде в системе WGS84 проецируются на плоскость карты так, как будто эти координаты определены на сфере радиусом R = a =  6 378 137 м (перепроецирование) — сферическое представление эллипсоидальных координат («spherical development of ellipsoidal coordinates«). Этой проекции, получившей название Web Mercator) соответствует EPSG (European Petroleum Survey Group) код 3857 («WGS 84 / Pseudo-Mercator«).
Перепроецирование из EPSG:4326 в EPSG:3857 ($\phi ,\lambda \rightarrow x,y  $) реализуется по вышеприведенным формулам для обычной сферической проекции Меркатора.
На такой карте направление на север всегда соответствуют направлению на верхнюю сторону карты, меридианы представляют собой равноотстоящие друг от друга вертикальные линии.
Но такая проекция в отличие от сферической или эллиптической проекции Меркатора не является равноугольной (конформной), линии румба в ней не являются прямыми. Линия румба (локсодром) — это линия пересекающая меридианы под постоянным углом.
Преимуществом рассматриваемой проекции является простота вычислений.

В указанной проекции карта может быть расчерчена прямоугольной сеткой координат (по значениям долготы и широты).
Привязку карты (сопоставление прямоугольных координат на карте и географических координат на местности) можно осуществить по $N$ точкам с известными координатами. Для этого необходимо решить систему из $2 N$ уравнений вида
$X = \rho_{\lambda} \lambda — X_0$ , $Y = arcsinh ( \tan ( \phi ) ) \cdot \rho_{\phi} — Y_0 $ .
Для решения системы уравнений и определения значений параметров $X_0$ , $Y_0$ , $\rho_{\lambda}$ , $\rho_{\phi}$ можно использовать, например, математический пакет Mathcad.
Для проверки правильности привязки карты можно определить отношение длин сторон прямоугольника построенной сетки. Если горизонтальная и вертикальная стороны прямоугольника соответствуют одинаковой угловой длине по долготе и широте, то отношение длины горизонтальной стороны (дуги параллели — малого круга) к длине вертикальной стороны (дуги меридиана — большого круга) должно быть равно $\cos \phi$ , где $\phi$ — географическая широта места.

Эллиптическая проекция Меркатора

Эллиптическая проекция Меркатора (EPSG:3395 — WGS 84/World Mercator) используется, например, сервисами Яндекс.Карты, Космоснимки.
Для эллиптической проекции действуют следующие формулы перевода широты $\phi$ и долготы $\lambda$ точки на поверхности земной сферы (в радианах) в прямоугольные координаты $x$ и $y$ на карте (в метрах):
$x = (\lambda — {\lambda}_0) \cdot a$ ;
$y = a \ln (\tan ({\pi \over 4} + {\phi \over 2}) ({{1 — e \sin {\phi}} \over {1 + e \sin {\phi}}})^{e \over 2} ) $ ,
где $a$ — длина большой полуоси эллипсоида, $e$ — эксцентриситет эллипсоида, ${\lambda}_0$ — долгота нулевого меридиана.
Масштабный коэффициент $k$ определяется выражением:
$k = {{\sqrt {(1 — {e^2} {{(\sin \phi)}^2})}} \over {\cos \phi}} $ .
Обратный перевод реализуется с помощью таких формул:
$\lambda = {x \over a} + {\lambda}_0 $ ;
$ \phi = {\pi \over 2} — 2 \arctan(e^{-y \over a} ({{1 — e \sin {\phi}} \over {1 + e \sin {\phi}}})^{e \over 2}) $ .
Широта вычисляется по итерационной формуле, в качестве первого приближения следует использовать значение широты, вычисленной по формуле для сферической проекции Меркатора.

Поперечно-цилиндрическая проекция Меркатора

Чаще всего используются две разновидности поперечно-цилиндрической проекции Меркатора — проекция Гаусса-Крюгера (англ. Gauss — Krüger) (получила распространение на территории бывшего СССР) и универсальная поперечная проекция Меркатора (англ. Universal Transverse Mercator (UTM)).
Для обеих проекций цилиндр, на который происходит проекция, охватывает земной эллипсоид по меридиану, называемому центральным (осевым) меридианом (англ. central meridian, longitude origin) зоны. Зона (англ. zone) — это участок земной поверхности, ограниченный двумя меридианами с разностью долготы в 6°. Всего существует 60 зон. Зоны полностью покрывают поверхность Земли между широтами 80°S и 84°N.
Отличие двух проекций заключается в том, что проекция Гаусса-Крюгера — это проекция на касательный цилиндр, а универсальная поперечная проекция Меркатора — это проекция на секущий цилиндр (для избежания искажений на крайних меридианах):

Проекция Гаусса-Крюгера

Проекция Гаусса-Крюгера была разработана немецкими учёными Карлом Гауссом и Луи Крюгером.
В этой проекции зоны нумеруются с запада на восток, начиная с меридиана 0°. Например, зона 1 простирается с меридиана 0° до меридиана 6°, ее центральный меридиан 3°.
В советской системе разграфки и номенклатуры топографических карт зоны называются колоннами и нумеруются с запада на восток, начиная с меридиана 180°.
Например, Гомель и окрестности относятся к зоне 6 (колонне 36) с центральным меридианом 33°.
Зоны/колонны делятся параллелями на ряды (через 4°), которые обозначаются заглавными латинскими буквами от А до V, начиная от экватора к полюсам.
Например, Гомель и окрестности относятся к ряду N. Таким образом, полное название листа карты масштаба 1:1 000 000 (10 км в 1 см), изображающей Гомель, выглядит как N-36. Этот лист делится на листы карт более крупного масштаба:

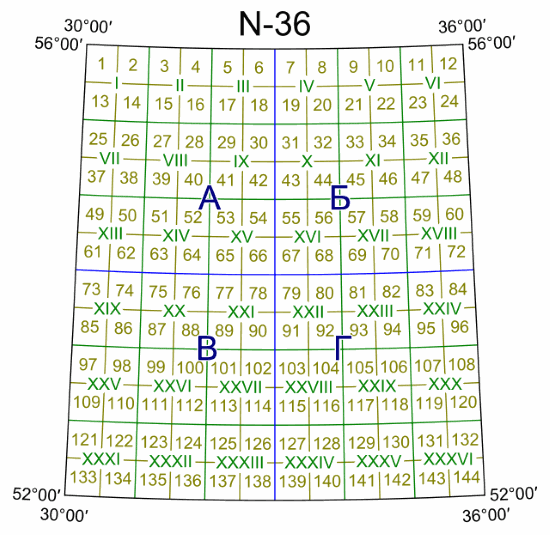
Для Беларуси и соседних стран разграфка такова:

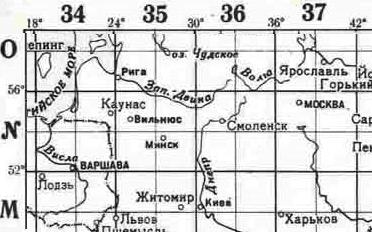
Для определения по топографической карте положения точки на карту наносят сетку прямоугольных координат X и Y, выраженных в километрах. Она образована системой линий, параллельных изображению осевого меридиана зоны (вертикальные линии сетки, оси X) и перпендикулярных к нему (горизонтальные линии сетки, оси Y).
На карте масштаба 1:200 000 расстояние между линиями сетки составляет 4 км; на карте масштаба 1:100 000 — 2 км.
Координата X подписывается на вертикальных краях листа карты и выражает расстояние до экватора, а координата Y подписывается на горизонтальных краях листа карты и состоит из номера зоны (первые одна или две цифры значения) и положения точки относительно центрального меридиана зоны (последние три цифры значения, причем центральному меридиану зоны присваивается значение 500 км).

фрагмент листа N36-123 советской топографической карты масштаба 1:100 000

Например, на вышеприведенном фрагменте карты надпись 6366 возле вертикальной линии сетки означает:  6 — 6-я зона, 366 — расстояние в километрах от осевого меридиана, условно перенесенного западнее на 500 км, а надпись 5804 возле горизонтальной линии сетки означает расстояние от экватора в километрах.

Универсальная поперечная проекция Меркатора

Универсальная поперечная проекция Меркатора (UTM) была разработана инженерными войсками США (United States Army Corps of Engineers) в 1940-х годах.

эмблема U.S. Army Corps of Engineers

Для построения карт в проекции UTM ранее использовался эллипсоид International 1924 — сетка UTM (International), а в настоящее время — эллипсоид WGS84 — сетка UTM (WGS84).
В этой проекции зоны нумеруются с запада на восток, начиная с меридиана 180°.
Эта система используется вооруженными силами США и НАТО (англ. United States and NATO armed forces):

Каждая зона разделена на горизонтальные полосы через каждые 8° широты. Эти полосы обозначены буквами, с юга на север, начиная от буквы C для широты 80° S и заканчивая буквой X для широты 84° N. Буквы I и O пропущены для избежания путаницы с цифрами 1 и 0. Полоса, помеченная буквой X, занимает 12° по широте.
Зона в этой проекции обозначается номером (англ. longitude zone) и буквой (каналом широты, англ. latitude zone):

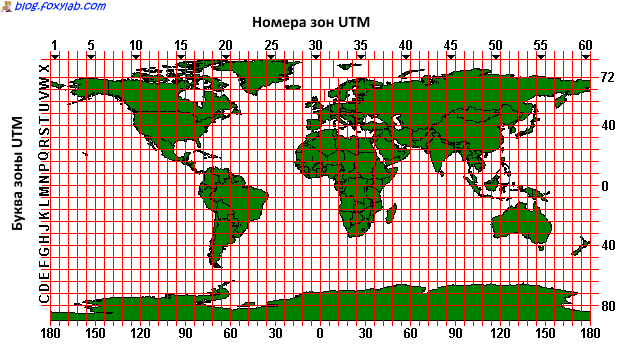
На этом рисунке видны две нестандартные зоны долготы — зона 32V расширена для покрытия всей южной Норвегии, а зона 31V сокращена для покрытия только водного пространства.
Для Гомеля и окрестностей зона обозначается как 36U с центральным меридианом 33°:

Зона покрывается прямоугольной (километровой) сеткой (сеткой по универсальной поперечной проекции Меркатора, СУППМ):

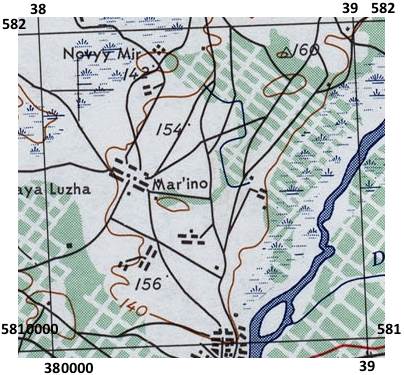
Длина стороны квадрата сетки в вышеприведенном фрагменте карты составляет 10 км.

Точка начала системы координат для каждой зоны определяется пересечением экватора и центрального меридиана зоны.
Координата E (Easting) на такой сетке представляет собой расстояние на карте от центрального меридиана в метрах (к востоку — положительное, к западу — отрицательное), к которому прибавлено + 500 000 метров (англ. False Easting) для избежания появления отрицательных значений.
Координата N (Northing) на такой сетке представляет собой расстояние на карте от экватора в метрах (к северу — положительное, к югу — отрицательное), причем в южном полушарии это расстояние вычитается из 10 000 000 метров (англ. False Northing) для избежания появления отрицательных значений.
Например, для левого нижнего угла квадрата сетки на вышеприведенной карте координаты записываются как
36U (либо 36+) 380000 5810000 ,
где 36 — longitude zone, U — latitude zone, 380000 — easting, 5810000 — northing.

Преобразование широты и долготы в координаты UTM поясняется рисунком:

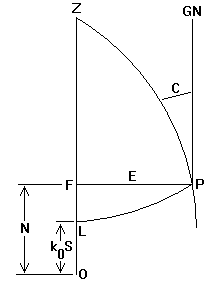
P — рассматриваемая точка
F — точка пересечения перпендикуляра, опущенного на центральный меридиан из точки P, с центральным меридианом (точка на центральном меридиане с тем же самым northing, что и рассматриваемая точка P) . Широта точки F (англ. footprint latitude) обозначается как $\phi ‘ $ .
O — экватор
OZ — центральный меридиан
LP — параллель точки P
ZP — меридиан точки P
OL = k₀S — дуга меридиана от экватора
OF = N — northing
FP = E — easting
GN — направление на север сетки карты (англ. grid north)
C — угол схождения меридианов (англ. convergence of meridians) —  угол между направлением на истинный север (англ. true north) и на север сетки карты

При преобразовании прямоугольных координат (X, Y) для проекции Гаусса-Крюгера на эллипсоиде WGS84 в прямоугольные координаты (N, E) для универсальной поперечной проекции Меркатора на том же эллипсоиде WGS84 необходимо учитывать масштабный коэффициент (англ. scale factor)  $k_0 = 0,9996 $ :
$ N = X \cdot k_0 $ ;
$ E = Y_0 + Y \cdot k_0 $ ,
где $ Y_0 = 500 000 $ метров.

Указанный масштабный коэффициент $k_0 = 0,9996 $ верен только для центрального меридиана зоны. При удалении от осевого меридиана масштабный коэффициент изменяется.

Примечание. Погрешность считывания координат с карты (georeferencing accuracy) обычно принимается равной ±0,2 мм. Именно такую точность имеют устройства, применяемые при создании аналоговой карты.

Геоид

Следует отметить, что более точным приближением поверхности нашей планеты является геоид (англ. geoid) — эквипотенциальная поверхность земного поля тяжести, т. е. поверхность геоида везде перпендикулярна линии отвеса. Но сила тяжести определяется векторной суммой гравитационной силы со стороны Земли и центробежной силы, связанной с вращением Земли, поэтому потенциал силы тяжести не совпадает с чисто гравитационным потенциалом.
Геоид совпадает со средним уровнем Мирового океана, относительно которого ведется отсчет высот над уровнем моря.
Геоид имеет сложную форму, отражающую распределение масс внутри Земли, и поэтому для решения геодезических задач геоид заменяется эллипсоидом вращения. Наиболее современной математической моделью геоида является EGM2008, пришедшая на смену популярной модели EGM96.

Продолжение следует.